Informatikai alapismeretek - Az információ
INF-2.3.2-M-2019/1.
(Az események információtartalma)[Előző oldal] --- [Következő oldal](A maximális entrópia)
2.3.2. Az entrópia
Eddig olyan példák kerültek szóba, amelyekben egyetlen esemény bekövetkezési valószínűségét, illetve az ebből eredő információtartalmat vizsgáltuk. Ha több esemény bekövetkezését vizsgáljuk, akkor eseményrendszerről beszélünk. Ha egy eseményrendszert n darab esemény alkot, és ebből kiválasztunk k darabot, ezek közül vagy egyik, vagy másik, vagy valamelyik (bármelyik) bekövetkezésének valószínűsége a k darab részesemény bekövetkezési valószínűségeinek összegével lesz egyenlő:
(7)
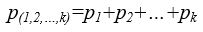 .
.
Tulajdonképpen a 4. sz. példa (páros számú pettyek dobása) kérdését is átfogalmazhatjuk úgy, hogy eseményrendszert alkosson a lehetséges kimenetelek száma: Mennyi a valószínűsége annak, hogy 2-est, vagy 4-est, vagy 6-ost dobunk? A megoldás magyarázata során már utaltunk erre a tényre, de ott még egy kalap alá vettük ezeket az eseményeket, és csak mint páros szám dobását fogalmaztuk meg a feltételt, nem volt jelentősége a részeseményeknek.
8. példa. Van 10 darab golyó egy dobozban: 1 fehér, 2 sárga, 4 piros, a többi kék. Mennyi a valószínűsége annak, hogy találomra kiválasztva egyet közülük, fehéret, vagy sárgát, vagy pirosat húzunk ki? Megoldás: a golyók száma: n=10, ezek között fehér: k(f)=1, sárga: k(s)=2, piros: k(p)=4 darab található. A három szín valamelyike közül történő húzás valószínűsége (5) és (7) képletekből adódóan:
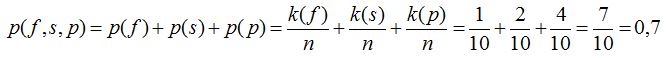 .
.
Ha a 3 db. kék golyó [k(k)=3] húzása is megengedett lenne, nyilván a biztos valószínűséget kapnánk, így alakulna a számítás:
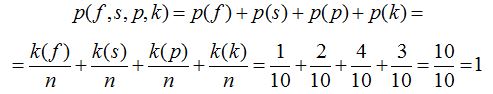 .
.
Általános esetben az n db. eseményt tartalmazó eseményrendszerről elmondható a megállapítás: A rendszer eseményeire vonatkozó összes valószínűség értéke 1, azaz, a biztos esemény.
(8)
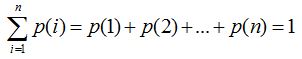 .
.
Ha feltételezzük, hogy a lehetséges esetek között nincs nulla valószínűségű esemény, és az összes esemény lefedi a teljes valószínűséget, azaz a (8) képlet érvényes a rendszerre, akkor számítható a rendszer információátlaga.
A rendszer átlagos információtartalmát, vagy más szóval várható értékét az események előfordulási valószínűségének és azok információtartalmának szorzatösszege adja. Ezt nevezzük entrópiának
(9)
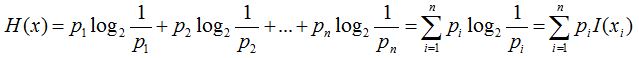 .
.
A (9) képletben a H(x) az entrópiát jelöli. A képlet segítségével számolható érték entrópia elnevezése a fizikából ismert entrópia képlethez való – pusztán formai – hasonlósága miatt adódott.
9. példa. Mennyi az entrópiája annak a rendszernek, amelyben p1=0,25; p2=0,25; és p3=0,5? A megoldás a (9) képletet felhasználva:
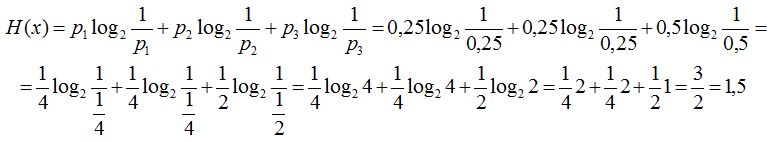 .
.