Informatikai alapismeretek - Az információ
INF-2.3.1-T-2019/1.
(Az információmennyiség mérése)[Előző oldal] --- [Következő oldal](Az entrópia)
2.3.1. Az események információtartalma
Az előző fejezetben láthattuk, hogy egyetlen esemény bekövetkeztével kapcsolatos értesülés információtartalma mikor 0 és mikor 1 [(1) és (2) képlet]. Továbbá az is megállapítást nyert, hogy több esemény esetén természetesen több bitnyi információ szükséges valamelyik kiválasztásához (pl. sok közül egy adott kártyalap kitalálásához). A hétköznapi életből azt is tudjuk, hogy minél több, egyforma eséllyel lejátszódható esemény bekövetkezte lehetséges, annál kisebb lesz ezek közül az egyik bekövetkeztének valószínűsége. A következőkben az események bekövetkezési valószínűsége, és azok információtartalma közötti összefüggésre mutatunk rá. Ezekhez felhasználjuk az eddigi megállapításainkat, illetve egyéb (tapasztalati, matematikai) ismereteinket is.
Emlékeztetőül: egy esemény bekövetkezésének valószínűségét (p) úgy számíthatjuk ki, hogy a kedvező esetek számát (k) osztjuk a lehetséges, azaz összes esetek számával (n). A jelölésekkel leírva a valószínűség: p=k/n. Bővítve egy kicsit a képletet, jelölve, hogy ezt egy adott ’x’ eseményre vonatkoztatjuk, akkor így alakul:
(5)
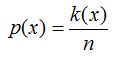 .
.
Néhány konkrét példa a képlet alkalmazására:
3. példa. Mennyi a valószínűsége egy adott lap kihúzásának egy magyarkártya-csomagból? Az (5) képletben az x esemény most egy adott lap húzását jelenti, de számunkra csak egy meghatározott lap lesz a jó, ezt jelöli a k(x)=1, és összesen 32 lap közül húzhatunk, ezért az n=32. Tehát a keresett valószínűség:
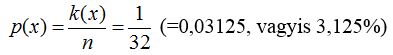 .
.
4. példa. Mennyi a valószínűsége, hogy egy dobókockával dobva páros számú pettyek kerülnek felülre? Az ’x’ esemény tehát a páros érték dobása. A kedvező esetek száma k(x)=3 (mert páros eredmény esetén 2, vagy 4, vagy 6 petty lehet felül), az összes lehetséges eset pedig n=6 (1, 2, 3, 4, 5, vagy 6 pettyet tartalmazó oldal valamelyike kerül felülre). Tehát a valószínűség:
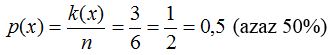 .
.
Belátható, hogy a páratlan számú érték dobásának valószínűsége pont ugyanannyi, mint a párosé, hiszen ott is 3 kedvező esetünk van. Ha pedig bármilyet dobhatunk, az hatféle érték lehet, s ekkor a valószínűség 6/6=1, tehát a biztos valószínűséget kapjuk, hiszen a hat közül valamilyen számú petty biztosan felülre fog kerülni. Ezt általános megfogalmazásban rögzíthetjük is:
A biztos esemény bekövetkezésének valószínűsége 1 (azaz 100 %). Ennek ellentéte az, hogy ha valamilyen esemény biztosan nem következhet be, akkor annak valószínűségi értéke 0.
Ha a köztes eseteket is vizsgálni akarjuk, akkor meg kell állapítanunk egy összefüggést. Ki kell tehát fejeznünk azt, hogy egy esemény bekövetkeztének információtartalma annál nagyobb, minél kisebb ennek az eseménynek a bekövetkezési valószínűsége. Egyszerű a megoldás, csak a már megállapított (4) képletben szereplő paramétereket kell a mostani fogalmainkkal egymásnak megfeleltetni. Ebben a k jelentette a kérdések számát, most pedig az I(x) információ nagyságot. A hatvány értéke a b, amelyet most a reciprok valószínűség fog megadni:
(6)
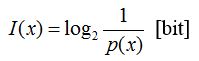 ,
,
ahol I(x) egy adott x esemény bekövetkeztének információtartalma, p(x) pedig az x esemény bekövetkeztének a valószínűsége. A gyakorlatban a (6) képlet számunkra azt jelenti, hogy minél váratlanabb (kevésbé valószínűbb) egy esemény bekövetkezte, az annál több információt hordoz. Azaz, ha p(x1)< p(x2), akkor I(x1)> I(x2).
További matematikai átalakításokat végezve a (6) képleten, az más alakra is hozható:
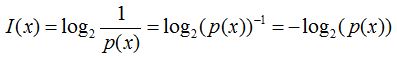 .
.
Nézzük meg ennek a képletnek a használatát néhány, korábban már említett esetre!
5. példa. Mennyi az információtartalma a biztos eseménynek? A biztos esemény bekövetkezési valószínűsége 100%, azaz p(x)=1. A (6) képlet alapján az információtartalom:
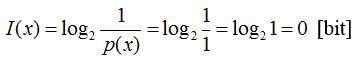 .
.
Tehát a biztos esemény információtartalma 0, ahogy ezt az (1) képlet már korábban jelezte. Erre példa, ha azt mondom, hogy holnap reggel felkel a nap, mert ez a tény biztos eseménynek tekinthető, de ezzel a kijelentéssel semmi újat nem mondtam, tehát nem kaptam információt (nem teljesült az információ egyik feltétele, az újszerűség).
6. példa. Mennyi az információtartalma annak a kijelentésnek, hogy egy érme feldobása után az ’írás’ oldal kerül felülre? Két eset lehet: fej, vagy írás (n=2). Az írás valószínűsége 50%, azaz p(x)=1/2. Ez az érték az (5) képletből adódik, de tapasztalatból is tudjuk. Így a kijelentés információtartalma:
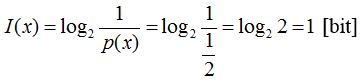 .
.
Az eredményt összevetve a (2) képlettel, azzal szükségszerűen egyezést látunk, azaz felére csökkentett bizonytalansággal 1 bitnyi információt szereztünk.
7. példa. Mennyi az információtartalma annak a kijelentésnek, hogy a 32 lapos magyarkártya-csomagból a piros királyt húztam? Fentebb már láthattuk (3. példa), hogy egy adott lap húzásának valószínűsége p(x)=1/32. Ezért a kijelentés információtartalma:
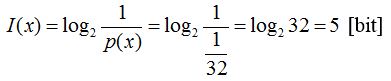 .
.
Másként fogalmazva, 5 bitnyi információ szükséges egy adott lap kitalálásához. Ezt az értéket fentebb már más módszerrel is megállapítottuk (lásd: 1. példa).
Megjegyzés: Eddigi példáinkban az előforduló események egyforma valószínűséggel szerepeltek. Ha különböző valószínűséggel következhetnek be események, akkor az azokhoz társítható információnagyság ugyancsak a (6) képlettel számítható, de természetesen előtte valószínűségszámítással kell meghatározni az adott eseményhez tartozó p(x) értéket.