CÍMLAP TARTALOM TÁRGYMUTATÓ MÉDIATÁR IRODALOM SZÓTÁR RÖVIDÍTÉSEK KÉRDÉSEK TESZT PDF PREZI SEGÉDLETEK

Informatikai alapismeretek - Az információ

INF-2.3-T-2019/1.

(Az információ további jellemzői)[Előző oldal] --- [Következő oldal](Az események információtartalma)

Mindennapos dolog, hogy két hír közül az egyik jobban érdekel minket, vagy többet tudunk meg általa, mint a másik révén. Felmerül a kérdés, hogy egy adott közleménynek mekkora az információtartalma. A hétköznapi értelemben használatos információ nagysága nehezen, vagy egyáltalán nem mérhető, de a legtöbb esetben nem is szükséges mérni, ezért nincs is erre elfogadott módszer. Például kevés értelme lenne meghatározni annak a hírnek az információtartalmát, hogy tegnap húsleves volt a menzán az ebéd. Mindezektől függetlenül van lehetőségünk az információ nagyságának mérésére. Méghozzá úgy, hogy a már emlegetett egyik jellemzőjét, az álala megszüntethető bizonytalanság nagyságát határozzuk meg.

Az információ nagysága mérhető. Mértékegysége a bit.

1 bit annak az információnak a nagysága, amelyet egy IGEN-nel, vagy NEM-mel megválaszolható kérdésre feleletül adunk (vagy kapunk).

A 'bit' szó önálló angol szóként is létezik és valaminek egy kis részét jelenti, de nem ebből a szóból származik az elnevezés, hanem itt a 'binary unit' (= kettes egység) szavakból keletkezett mértékegységről van szó. Ez két, azonos valószínűséggel bekövetkező esemény közül az egyik (bármelyik) bekövetkeztének a mértékét jelenti. Tehát, ha felteszünk egy eldöntendő jellegű kérdést, mint pl. esik-e kint az eső, akkor a rá kapott 'igen' vagy 'nem' válasz pontosan egy bitnyi információt hordoz.

A fenti példához több hasonló, két lehetséges kimenetelű eseményt említhetünk, mint például a pénzfeldobás 'fej, vagy írás' esetét, vagy a barkochba játék szabályát, ahol a kérdésekre csak 'igen' és 'nem' válaszokat lehet adni. Viszont a legtöbb esetben nem pusztán két kimenetelűek az események, valamint azok bizonytalanságának a mértéke is különböző lehet. Minél több lehetséges kimenetelű egy esemény, vagy minél több feltételnek kell egyszerre teljesülnie valamelyiknek a bekövetkeztéhez, a hozzá társítható információ annál nagyobb bizonytalanságot szüntet meg. Így ilyen esetben nagyobb mennyiségű információhoz juthatunk az adott dolgot illetően. Ezeket meggondolva megállapíthatjuk a következőket:

Egy adott 'x' esemény 'I(x)' információtartalma legyen 0, ha nem csökkenti a bizonytalanságot:

(1)

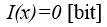
Ha például azt a kijelentést tesszük, hogy 'holnap reggel felkel a nap', akkor ezzel semmi újat nem állítunk, hiszen évmilliók óta így van, és semmi sem utal arra, hogy ez holnapra másként lesz, tehát biztosan bekövetkező eseményt közöl a kijelentés, így semmiféle új információhoz nem jutunk.

Egy adott 'x' esemény 'I(x)' információtartalma legyen 1, ha felére csökkenti a bizonytalanságot:

(2)

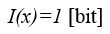
Hogy miért pont a felére? Mert az 'igen' vagy 'nem' válaszok a két (egyformán bekövetkezhető) eset közül az egyiket, azaz a lehetséges kétféle kimenetelnek a felét jelentik. Természetesen egyes események különböző valószínűséggel is bekövetkezhetnek, de ezzel kicsit később fogunk foglalkozni. Egyelőre induljunk ki az egyszerűbben kezelhető, azonos valószínűséggel bekövetkező esetek vizsgálatából. Nézzünk egy példát!

1. példa. Hány bitnyi információra van szükségünk ahhoz, hogy egy 32 lapos magyar kártyából egy tetszőlegesen kiválasztott lapot meg tudjunk nevezni? A játékszabály: csak olyan kérdést lehet feltenni, amire 'igen' vagy 'nem' válaszok adhatók, azaz egy kérdésre pontosan egy bitnyi választ kapunk. Így nyilván a kitaláláshoz szükséges kérdések száma adja meg a keresett információ nagyságát. Gondoljunk a feladványban pl. a piros királyra!

• Legyen az első kérdésünk (amivel máris felére csökkentjük a lehetséges lapok számát): 'A piros vagy makk színek közé tartozik a kitalálandó lap?' Erre természetesen 'igen' lesz a felelet. De belátható, hogy ha zöld és tök színekre kérdezünk rá, akkor a 'nem' válasz terel majd minket a jó irányba. Tehát teljesen mindegy, hogy melyik színpárra vonatkozóan tesszük fel a kérdést.
• Második kérdés: 'Makk a szín?' Erre most 'nem' választ kapunk, tehát máris tudjuk, hogy piros a kártya színe. A következő kérdéssel felezzünk tovább a megmaradt lapok számát!
• Harmadik kérdés: 'Számok találhatók a lapon?' A felelet 'nem' lesz, hiszen figurás lapról van szó.
• Negyedik kérdés: 'Alsó, vagy felső közül valamelyik?' A válasz megint csak 'nem' lesz. Tehát már tudjuk, hogy vagy piros király, vagy piros ász a kitalálandó lap. Az egyikre rákérdezünk.
• Ötödik kérdés: 'A piros király a kitalálandó lap?' 'Igen!' - kapjuk a választ, és már ki is találtuk a lapot. Ha véletlenül a piros ászra kérdezünk, akkor sincs baj, mert a 'nem' válasz után már úgyis csak a piros király marad, tehát nem kell több kérdés a lap kitalálásához.

Állapítsunk meg valamilyen törvényszerűséget a szükséges kérdésszámot illetően! Egyetlen lehetséges eset kitalálásához nyilván nem kell kérdés, azaz a kérdések száma 0. Amint már láttuk, ez a biztos eset, mert csakis egy kimenetele lehet, tehát információtartalma 0. Két lehetséges esetben egy kérdés kell, hogy eldönthessük, melyik következett be. Például a már emlegetett érme feldobásnál. Három esetben már két kérdést kell feltennünk, 2+1 részre bontva a lehetséges eseteket. De ugyancsak elég két kérdés 4 lehetséges esetben, mert azt az első kérdéssel felezve, azaz 2+2-re bontva a teljes tartományt, a helyes irányban megint csak további egy kérdés kell a maradékból való választáshoz. Ugyanilyen megfontolásból megállapítható, hogy az előbbi példában szereplő 32 lapos kártya helyett egy 64 különböző lapos kártyapakli esetén az öt kérdés helyett csak eggyel többre, azaz hatra van szükségünk egyetlen lap kitalálásához, hiszen az első kérdéssel megfelezzük a 64 lapot, így máris csak az egyik 32 lapos csomagunk marad, amihez láthatóan 5 kérdés elegendő. Az alábbi táblázat jól mutatja a törvényszerűséget.

1. sz. táblázat. Elemek és kérdések száma közötti összefüggés.

Észrevehető, hogy a szükséges kérdések száma egy adott elem kitalálásához éppen a 2 hatványkitevője. Pl. ha valaki gondol egy egész számot 1 és 1024 között (beleértve a tartomány határait is), akkor a tartományok felezésének módszerével 10 kérdésből a gondolt szám kitalálható. Az első kérdés legyen például: A gondolt szám 1 és 512 között van? A kapott válasznak megfelelően vagy az első 512, vagy a második 512 (513 és 1024 között) számtartományban van a gondolt szám, tehát máris csak az eredeti mennyiség fele között kell tovább keresnünk. A 10 kérdés azt jelzi, hogy ennyi igen-nem felelet, azaz 10 bitnyi információ szükséges az adott szám kitalálásához.

De mi van abban az esetben, ha nem a kettő egész hatványaival (lásd az 1. sz. táblázat első oszlopa) egyezik meg a választható elemek száma? Nos, számoljunk kicsit! Láthattuk, hogy a szükséges kérdésszámot illetően tulajdonképpen hatványkitevő keresésről van szó, amit a matematikában a logaritmus definíciójából már jól ismerünk. Emlékeztetőül: log_ab –vel jelöljük azt a k kitevőt, amelyre az a alapot emelve b-t kapunk. Ez a definíció az

(3)

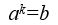
képletből adódik, melyől kifejezve a k-t az alábbi alakot kapjuk:

(4)

ahol k a szükséges kérdések mennyiségét, a b az elemek (esetek) számát jelöli, és mivel a felezéses módszer miatt a példáinkban kettő hatványaival számoltunk, a logaritmus alapja a=2 lesz. Az előbbi, 1024 számból való kitalálási példánál maradva a (4) képlet alapján így fogalmazhatjuk meg a válaszunkat: k=log₂1024 bitnyi információra van szükségünk egy szám kitalálásához. Ennek az egyenletnek a megoldása még fejben is megy, hiszen könnyen kiszámíthatjuk, hogy kettőt hanyadikra kell emelni, hogy 1024 legyen az eredmény. Így k értékére hamar megkapjuk a 10-es végeredményt, hiszen 2¹⁰=1024. Ez egyébként az 1. sz. táblázatból is kiolvasható. De volt egy nyitva maradt kérdésünk: Mi a helyzet, ha nem 2 egész értékű hatványszámáról van szó? A választ akövetkező példán szemléltetjük.

2. példa. 100 lehetséges szám esetén hány bitnyi információra van szükség egynek a kitalálásához? A (4) képletet felhasználva a megoldást a k=log₂100 egyenlet adja. Ebben a k értékének kiszámításához már függvénytáblázat, számológép, vagy számítógép segítsége szükséges, bár az 1. sz. táblázat alapján egy nagyságrendi sejtésünk már előzetesen is lehet. Ugyanis a 100-as elemszám a 64 és a 128 közé esik, így a log₂100 értéke is a log₂64-hez tartozó 6, és a log₂128-hoz tartozó 7 értékek közé kell essen, és közelebb lesz a 7-hez, mint a 6-hoz. A keresett, hat tizedes jegyre pontos eredmény:

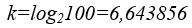
Természetesen ez csak egy elméleti érték, mert törtszámú kérdést nem tudunk feltenni, és látjuk, hogy 6-tól több kell, tehát 64 felett 128-ig 7 kérdésre van szükségünk egy szám kitalálásához.

Egy megjegyzés, segítségül azok számára, akik ellenőrizni szeretnék a fenti eredményt, illetve azoknak, akiknek kedvük van a számolgatáshoz: Nem nagyon találunk függvénytáblázatokban kettes alapú logaritmustáblázatokat, csak tízes alapúakat, vagy e alapút. Többnyire a számológépek sem rendelkeznek ilyen funkcióval, csak a drágább kategóriájúak. Átírni ugyan át lehet másik alapra egy logaritmusos kifejezést, de ez dupla számításigényű eljárás (ehhez a log_bx=log_ax/log_ab képletet kell alkalmazni). Viszont sok számítógépen elérhető egy táblázatkezelő program, amiben egyszerű képlet segítségével megkaphatjuk a keresett eredményt. Pl. a MS Excel egy cellájába beírt '=LOG(100;2)' kifejezés kiértékelése a 100-as érték 2-es alapú logaritmusát adja vissza, a fenti példában számolt eredménnyel.