Informatikai alapismeretek - Az információ
INF-2.3.3-M-2019/1.
(Az entrópia)[Előző oldal] --- [Következő oldal](Relatív entrópia)
2.3.3. A maximális entrópia
Egy rendszernek akkor a legnagyobb az entrópiája, ha az egyes események bekövetkezési valószínűsége azonos, azaz p1=p2=...= pn=p. Ekkor az (5) és (9) képletek alapján:
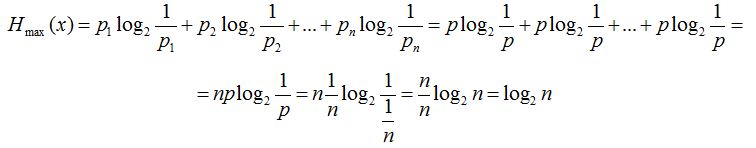 .
.
Tehát
egy n elemű rendszer maximális entrópiája:
(10)
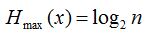 .
.
10. példa. Mekkora lehetne a 9. példában szereplő eseményrendszer maximális entrópiája? Mivel 3 esemény alkotja az eseményrendszert, ezért p1=p2=p3=1/3 esetben lenne maximális az entrópia:
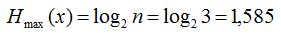 .
.
Ezek ismeretében érthető, hogy egyezést találunk egy eseményhalmaz azonos valószínűséggel bekövetkezhető valamelyik eseményének információtartalma és a szóban forgó rendszer maximális entrópiája között. A 7. példában a 32 lapos kártyacsomag egy lapjának húzási valószínűsége 1/32 volt, az egyik lap megnevezése pedig a kijelentés 5 bitnyi információtartalmát jelentette. A rendszert alkothatja mondjuk az a kijelentés halmaz, amely sorra megnevezi, hogy melyik lapot húztam. Ez nyilván n=32 kijelentés. (A 7. példában csak a piros király húzása szerepelt.) Eme rendszer maximális entrópiája:
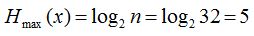 .
.